Textures in the previous post allow the drawing of tiles, but the aspect ratio is not correct. In this post, I show how to draw a tile on a grid location correctly.

This post is part of the OpenGL 2D Facade series

Objective

We wish to draw a tile from a tileset to a grid location on the screen:

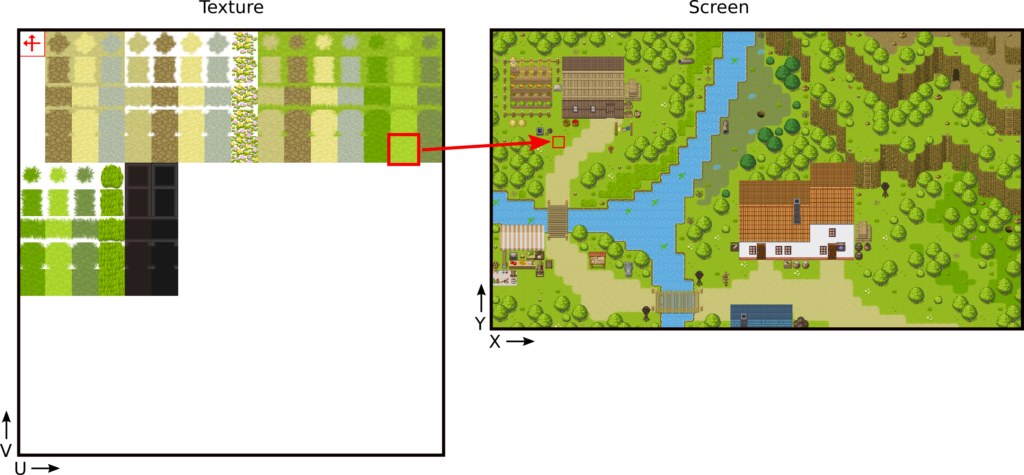
Note: I use free tiles created by Pipoya. I extracted some of them to build a tileset for this post; you can find more on the itch.io page: pipoya.itch.io/pipoya-rpg-tileset-32x32.

Texture coordinates

The texture contains the image tileset. There are many tiles of the same size: 32x32 pixels. They are all aligned on a regular grid, so each tile coordinate is a multiple of their size. For instance, the grass tile surrounded by a red box is on the 15th row of the 5th column, so the coordinate of its top-left corner is 1432=448 per 432=128 (remind that coordinate starts at 0: the coordinate of the first column is 0, the second is 1, and so on).

As a result, we can identify any tile in the tileset by grid coordinates, and then easily deduce their pixel coordinates using the tile size. The grass tile in the red box has grid coordinates (14,4) and pixel coordinates (448,128). This property is attractive because we can easily replace a tileset with another one of higher resolution without changing the code.

Unfortunately, these coordinates are not the ones expected by OpenGL: it requires float values between 0 and 1 (the UV coordinates), whatever the image resolution. Consequently, we need another conversion from pixel coordinates to UV coordinates. This one is easy: we only need to divide the pixel coordinates by the size of the texture. In this example, the size of the tileset image is 512x512 pixels. The UV coordinates of the grass tile in the red box are 448/512=0.875 per 128/512=0.25.

In the end, we can directly compute the UV coordinates from the grid coordinates, using tile size in UV coordinates. In this example, since the tile size is 32x32 and the texture size is 512x512, then the UV tile size is 32/512=0.0625 per 32/512=0.0625. For the grass tile in the red box, the UV coordinates are 140.0625=0.875 per 40.0625=0.25.

Note: Please remind that I assume that we flip the texture so we can consider top-down V coordinates. Without this assumption, and since OpenGL uses bottom-up V coordinates, we should invert them (compute 1.0-V). For the grass tile in the red box, the UV coordinates become 0.875 per 1.0-0.25=0.75.

Screen coordinates

For the screen coordinates, I assume that the size of the rendering area is a multiple of tile sizes. I also assume that we render tiles on a regular grid. These assumptions ease the understanding of coordinates computations; we'll see in the next posts how to handle more complex cases. In the example, the rendering area has 60x33 tiles, and therefore a resolution of 6032=1980 per 3332=1056 pixels.

We can compute the pixel coordinates of any grid tile as with the texture: just multiply the grid coordinates by the tile size. The grass tile in the red box in the screen has grid coordinates of (7,12) and thus pixel coordinates of 732=224 per 1232=384.

As for UV coordinates, we have to convert pixel coordinates into float values for OpenGL. In the screen case, values are from -1 to 1 (instead of 0 to 1). The computation of the OpenGL X coordinate is then: -1 + 2pixel coordinates/screen width. For the OpenGL Y coordinate, since the values are bottom-up, the computation is inverted: 1 - 2pixel coordinates/screen height. The grass tile in the red box has OpenGL coordinates -1 + 2224/1980=0,773 per 1 - 2384/1056=0,272.

We can also directly compute the OpenGL screen coordinates from the grid coordinates using the tile size in OpenGL screen coordinates. This tile size is twice the pixel tile size divided by the screen size. In this example, it is 232/1980=0,0323 per 232/1056=0,0606. We can recompute the OpenGL screen coordinates of the grass tile: -1 + 70,0323=0,77 per 1 - 120,0606=0,272.

Draw a single tile

Let's now update the code from the previous post to draw one tile from the tileset to a grid location on the screen.

Tile and window sizes

We first create the window:

tileWidth = 32
tileHeight = 32
screenWidth = tileWidth * 3
screenHeight = tileHeight * 3
screenTileWidth = 2 * float(tileWidth) / float(screenWidth)
screenTileHeight = 2 * float(tileHeight) / float(screenHeight)
screenSize = (screenWidth, screenHeight)
pygame.display.set_mode(screenSize, pygame.DOUBLEBUF | pygame.OPENGL)
pygame.display.set_caption("OpenGL 2D Facade - https://www.patternsgameprog.com/")

The two first lines define the pixel size of the tiles. I highly recommend storing this kind of values in variables. It eases a lot the reading of expressions and usually leads to no computation overhead. Furthermore, it will be effortless to change the size of the tiles if needed.

Lines 3-4 compute the window/screen size. In this post, we constraints ourselves to a window size that divide the size of the tiles to simplify the formulas (we'll see in next posts more complex cases). In this example, we selected a window of 3 per 3 tiles. Feel free to change this size to see what happens.

Lines 5-6 compute the tile sizes in OpenGL screen coordinates. We will use these values to convert grid coordinates to OpenGL screen coordinates.

The last lines create the window using the size we computed.

Texture image

We load the texture image and set some variables:

image = Image.open("ground.png")
assert image.mode == "RGBA"
textureWidth = image.size[0]
textureHeight = image.size[1]
textureTileWidth = float(tileWidth) / float(textureWidth)
textureTileHeight = float(tileHeight) / float(textureHeight)
imageArray = np.array(image)

Lines 1-2 load the texture image as before.

Lines 3-4 get the pixel size of the image.

Lines 5-6 compute the UV tile size. We use these values to convert grid coordinates to UV coordinates.

Line 7 converts the PIL image into a Numpy array.

Mesh vertices

We consider a single rectangle, so we need four 2D points:

spriteGridX = 1
spriteGridY = 1
spriteScreenX1 = -1 + spriteGridX * screenTileWidth
spriteScreenY1 = 1 - spriteGridY * screenTileHeight
spriteScreenX2 = spriteScreenX1 + screenTileWidth
spriteScreenY2 = spriteScreenY1 - screenTileHeight
vertices = np.array([
    [spriteScreenX1, spriteScreenY2],
    [spriteScreenX1, spriteScreenY1],
    [spriteScreenX2, spriteScreenY1],
    [spriteScreenX2, spriteScreenY2],
], dtype=np.float32)

Lines 1-2 define the grid coordinates on the screen. We only consider this case to ease the understanding; we will see more complex cases in the next posts. You can try other coordinates (like (0,1) or (2,0)) to see what happens.

Lines 3-4 define the top left corner of the rectangle. It is the application of the formula presented in the previous section.

Lines 5-6 define the bottom right corner of the rectangle. It is the sum of the top left corner and the size of a tile. For the Y-axis, we subtract since OpenGL uses bottom-up vertical coordinates.

The last lines define the vertices. Note that we swap Y coordinates also because OpenGL has bottom-up vertical coordinates.

Texture UV coordinates

As for the vertices, we only consider coordinates on a grid:

spriteTileX = 0
spriteTileY = 0
spriteTextureX1 = spriteTileX * textureTileWidth
spriteTextureY1 = spriteTileY * textureTileHeight
spriteTextureX2 = spriteTextureX1 + textureTileWidth
spriteTextureY2 = spriteTextureY1 + textureTileHeight
uvMap = np.array([
    [spriteTextureX1, spriteTextureY2],
    [spriteTextureX1, spriteTextureY1],
    [spriteTextureX2, spriteTextureY1],
    [spriteTextureX2, spriteTextureY2],
], dtype=np.float32)

Lines 1-2 define the grid coordinate of the tile to use. You can try other coordinates (like (4,14) the grass tile) to see what happens.

Lines 3-6 define the top left and bottom right corners of the tile. It is similar to the previous case, expect that UV coordinates are between 0 and 1, and Y-axis is not inverted (thanks to a loading of a reversed texture image).

The last lines define the UV coordinates. Note that Y values are also inverted, even using a reversed texture image, because OpenGL read order is also bottom-up.

Mesh vertex indices

We consider a single rectangle, the list of vertex indices is elementary:

faces = np.array([
    [0, 1, 2, 3]
], dtype=np.uint)
faceCount = faces.shape[0]

Final program

Download code and assets

The program displays a single tile in the middle of the window:

I created this tile to check that the rendering is correct: the arrows must point to the left and the top of the window.

In the next post, I'll show how to render a level created with Tiled.